Saturated Packings and Voronoi Cells
© Copyright, 1996, Eric Harshbarger
Table of Contents
Introduction
This page addresses a problem which I first encountered as a graduate student at Auburn University attending a geomtrey class taught by Dr. W. Kuperberg. While I did not solve the problem (stated below) completely at the time, it continued to pique my curiousity every once in a while even though I was no longer entrenched in Mathematics as I was back in 1994. Upon revisiting the problem recently I actually stumbled across a way to solve it completely. That is what I am including on this page. First, however, I will establish a few definitions. As stated before, my days of 'heavy Math' are a couple years past now, so forgive any informal feel of the presentation... Also, because of the character set limitations of HTML documents, I will be using non-traditional notation for some of the mathematical concepts. Where it deviates from the norm, I will try to explain the notation appropriately. -- ech
Definitions
The problem stated below will deal with saturated packings of the plane by unit circles. A packing of the plane with unit circles is simply a configuration of unit circles (radius=1) in the plane such that no interiors of two distinct circles intersect. Two circles may 'kiss' by being tangent to one another, but their interiors must be disjoint. For such a packing to be saturated means that if any (unit) circle is added to the packing, the new circle will necessarily overlap one of the circles already in the plane.
A easy visualization is scattering numerous pennies onto a tabletop. If all pennies lie flat on the table (none on top of another), that is a packing. If the pennies are arranged so that no additional pennies may be laid on the table (without overlapping part of an existing penny), the packing is saturated.
Next, the idea of a Voronoi Cell needs to be defined. Given a set of points P = {p0, p1, p2, ...} in a plane, one can partition the plane into Voronoi Cells (polygons) such that a Voronoi Cell about a point p in P consists of all points in the plane which are closer to p than any other point in P. The edges of a polygonal Voronoi Cell represent all points equidistant of two points in P, and vertices where three or more edges meet indicate a point which is equidistant of three (or more points) in P. An edge (say between p0 and p1) of a Voronoi Cell is clearly a line segment which is a subset of the perpendicular bisector of the line segment connecting p0 and p1.
The Question
Suppose S is a satured packing of the plane by unit circles, and V is the partitioning of the plane into Voronoi Cells about the centers of the circles. What is the maximum number of sides that any of the Voronoi Cells of V can have?
The problem may have its focus narrowed to simply seeing how many circles one can 'squeeze' around a central circle to force that central circle to have a many-sided Voronoi Cell. What occurs outside of this 'ring' of circles is more or less inconsequential... it is easy enough insure that the packing is saturated outside of the ring. The trickiness of constructing this ring of circles about a central circle is that one must find a compromise between packing as many circles as possible while making sure that each circle, in fact, contributes an edge to the resulting Voronoi Cell about the central circle. The danger is that a particular circle's neighbors may 'cut off' it's contribution if these neighbors are positioned too closely (for example) to the central circle. And, of course, one cannot use an arbitrarily large number of circles in the ring since geometrically the resulting ring might leave too much space vacant, violating the saturated condition.
So, the problem can be attacked from two directions: providing examples of valid constructions that increase the lower bound on the number of possible sides, and decreasing the upper bound by proving that too many circles will necessarily 'unsaturate' the packing, or will at least not help by contributing additional sides to the central Voronoi Cell.
Working up to a lower bound.
It is easily shown that 11 unit circles can be arranged equidistantly around a central circle such that they satisfy the conditions of the question. The resulting Voronoi Cell is a regular 11-gon. Simple distance calcutations show that the ring is saturated in the sense that another circle will not 'fit' between the ring of 11 and the central circle.
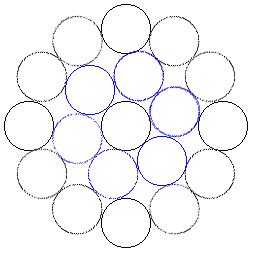 Trying to place 12 circles equally about the central circle (to form a regular dodecagon Voronoi Cell) yields an invalid arrangement. The illustration proving its unsaturated state is quite pretty (see Figure); it was shown to me during the MH639 class by W. Kuperberg.
Trying to place 12 circles equally about the central circle (to form a regular dodecagon Voronoi Cell) yields an invalid arrangement. The illustration proving its unsaturated state is quite pretty (see Figure); it was shown to me during the MH639 class by W. Kuperberg.
The question then comes up, however, as to whether one could shift the 12 circles slightly so as to keep 12 sides to the central Voronoi Cell (though not regular -- regularity is not a necessary condition), but blocking the vacant space available in the regular dodecagon example. The fit of the interior circles in the illustration is exact. There is no extra room, so one might think that it is possible to alter the configuration oh-so slightly.
After (way too) many rearrangements (and many distance/line calculations) no increase of the lower bound was made, so I then decided to leave the lower bound at 11 and start approaching the problem from the top... and go down on the upper bound.
Lemma 1
The following lemma will be useful not only for this problem, but also in the 3 dimensional version as well. For notation, d(x,y) denotes the distance between two points, x and y; >, <; refer to strict inequality, and >=, <= are used to refer to 'soft' inequalities.
LEMMA 1. Let p1 & p2 be points in a standard Cartesian Plane. Let l1 and l2 be the line segments joining p1 with the origin (p0) and p2 with the p0, respectively. Let m1 and m2 be the perpendicular bisectors of l1 and l2, respectively. Let angle A be the angle formed by l1 and l2. Under the following conditions:
- p1 = (0,b) where b > 0 (p1 lies on the positive y-axis)
- p2 = (c,d) where c > 0, d > 0 (p2 lies in Quadrant I)
- 2 <= d(p0, p1) < 4
- 2 <= d(p0, p2) < 4
- 2 <= d(p1, p2)
- 2 >= d(p0, v) where v is the intersection point of m1 & m2
the measure of A > 30°.
Proof: From condition 5, we get:
- 4 <= c2 + (b-d)2
The equations of m1 and m2 are:
- m1: y = b/2
- m2: y = (-c/d)x + (c2 + d2)/2d
And so:
- v = ( (c2 + d2 - bd)/2c , b/2 )
- (((c2 + d2 - bd)/2c)2 + (b/2)2)½ < 2 (by condition 6)
From this we get:
4 > (b/2)2 + ((c2 + d2 - bd)/2c)2
= b2c2/4c2 + (c4 + c2d2 - 2c2bd + d4 + c2d2 - 2bd3 + b2d2)/4c2
= (c2(c2 + d2 - 2bd + b2) + d2(c2 + d2 - 2bd + b2))/4c2
= (c2 + d2)(c2 + d2 - 2bd + b2)/4c2 (by i. we get next)
>= (c2 + d2)(4)/4c2
= (c2 + d2)/c2
= 1 + (d/c)2
implying
-3½ < d/c < 3½
but d/c is simply the slope of line segment l2 and since arctan(3½) = 60°, the angle formed by line segment l2 and the positive x-axis must be strictly less that sixty degrees, this implies that the angle A must be strictly greater than 30°.
q.e.d.
Working down on a upper bound.
An immediate candidate for an upper bound may be found by considering this estimate:
A quick upper bound
Any circle c1 which is to contribute a side the central Voronoi Cell must have it's center less than distance 4 from the center of the central circle (c0). This is clear, for if the distance between centers were greater than or equal to 4, the edge of the central Voronoi Cell would necessarily have a point greater than or equal to a distance of 2 not only from c0 and c1's centers, but also all other centers of the other circles (by the construction of the Voronoi Cells in the first place). But this would mean that a unit circle could be centered at such a point without intersecting the other circles... contradicting the saturation requisite. Thus, all of the centers must be contained in a circle of radius 4 centered at the center of c0. This means the interiors of all of the circles must lie with a circle of radius 5 (the packing circles are unit circles, remember).
The area of the circle of radius 5 centered at the center of c0 is 25*PI. The area of a unit circle is PI. Thus, one can crudely estimate that no more than 25 circles can be packed into the circle of radius 5... meaning that at most 24 sides could appear on the Voronoi cell about one of the circles (25 circles, but a 'central' circle will not add another side to its own Voronoi Cell by itself).
This is a very rough bound, but it is a start.
A better upper bound
PROPOSITON 1: Assume S is a saturated packing of a plane by unit circles, and V is the Voronoi Partitioning of the plane about the centers of those circles. The maximum number of sides any Voronoi Cell of V may have is 11.
Proof: Let c0 be a 'central circle' around which circles (c1, c2, ..., cn) each contribute a side to the Voronoi Cell about c0. Assume n is the maximum integer such that each circle so contributes. Consider two circles of the ring (say, cj and ck) such that
cj and ck are 'immediate neighbors in the ring' in the sense that if one forms a line segment for each ring-circle by connecting its center with the central circle's center (labeled l1, l2,... ln), there exists no integer i such that li divides the angle formed by lj and lk.
One may orient a Cartesian Plane coordinate system such that the center of c0 is the origin, the center of cj lies on the positive y-axis, and the center of ck lies in Quadrant I (the center of ck cannot be on the positive y-axis (no room); if ck's center is in Quadrant II, reflect by symmetry without loss of generality; if the center of ck lies below the x-axis, it is clear that n is not maximal).
By the construction methods of Voronoi Cells, and the fact that the packing of the plane is saturated, all of the conditions of Lemma 1 are met.
This implies n must be (strictly) less than 12 since the angle between any two line segments lj and lk must be greater that 30°
q.e.d.
The Answer
Since 11 has been shown to be both an upper and lower bound on the number of circles which may situated about a central circle in a saturated packing such that each circle contributes a side to the Voronoi Cell about the central circle, the answer to the Question is 11.
In Three Dimensions
The question above may be generalized to higher dimensions of geometric space. Specifically, one may ask the following:
Suppose S is a satured packing of 3-space by unit spheres, and V is the partitioning of space into Voronoi Cells (polyhedra) about the centers of the spheres. What is the maximum number of faces that any of the Voronoi Cells of V can have?
Often when one extrapolates from 2 to 3-space analogous problems get messier. This is no exception. The best that I have been able to get on this problem is a range of possible solutions based on a lower bound and upper bound. The two bounds are 'close' to one another, but not equal yet. Let's start at the bottom end first.
A lower bound in 3D
Consider the following collection of points:
- (±3.40, ±1, ±1), (±1, ±3.40, ±1), (±1, ±1, ±3.40) -- 24 total
- (±2.50, ±2.50, 0), (0, ±2.50, ±2.50), (±2.50, 0, ±2.50) -- 12 total
- (±2.08, ±2.08, ±2.08) -- 8 total
It is easily calculated that all of the points are within distance 4 of (0,0,0), but not nearer than 2. Furthermore, each is at least distance 2 from one another. Also, if one considers the line segments joining each point with the origin, it may be checked that each midpoint of each line segment is nearer to the origin and opposite endpoint than it is to any of the other points (strictly nearer). This demonstrates that each sphere does, in fact, contribute a side to the Voronoi Cell surronding the central sphere.
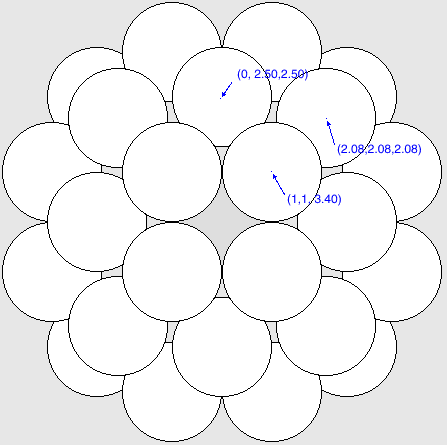
Finally, it is necessary to show that the 'shell' of spheres saturates the area about the central sphere in the sense that an additional sphere may not be placed within the shell. This can be done fairly easily (calculations will be provided soon).
Thus, a lower bound of 44 is obtained for the problem.
An upper bound in 3D
PROPOSITION 2: Assume S is a saturated packing of 3-space by unit spheres, and V is the Voronoi Partitioning of 3-space about the centers of those spheres. The maximum number of faces any Voronoi Cell (polyhedron) of V may have is 58.
Proof: Let s0 be a 'central sphere' about which n spheres (s1, s2, ..., sn) are situated such that each contributes a face to the Voronoi Cell about s0 and n is the maximum integer for which those conditions hold. Let l1, l2, ... ln be the line segments connecting the center of s0 with s1, s2, ..., sn (respectively), and q1, q2, ... qn be the planes which are perpendicular to, and pass througn the midpoint of, l1, l2, ..., ln repsectively. Orient a Cartesian coordinate system such that s0 is centered at (0,0,0), si (1 <= i <= n) is at (0,y,0) with y > 0, and let sj be the 'nearest' sphere to si ('nearest' meaning that the angle formed by li and lj is not larger than the angle formed by li and any other line segment lk (1 <= k <= n)).
Since sj is nearest to si, qj and qi necessarily form an edge, e, of the Voronoi Cell about s0. Furthermore, e must be an actual line segment (not just a point). Any point on e must lie within distance 2 of (0,0,0); as must the point, p, on the line containing (extending) e which is closest (and equidistant) from the centers of s0, si, sj (note a proof that p is actually on e is not given -- nor is it necessary).
Consider the plane which contains the centers of s0, si, sj. This will necessarily contain li, lj, and p. Furthermore, these centers of s0, si, sj, and the point p satisfy the conditions of Lemma 1 (note that the center of sj must lie in Quadrant I (or at least QII -- symmetric) in order for n to be maximal). This shows that the lines l1, l2, .. ln must all be at least 30° apart from one another.
Now imagine if those line segments were extended radially away from the origin so that they intersected a sphere of radius 4 about the origin. The measures of the angles between the lines would not change. Furthermore, each of those intersection points (call them t1, t2, ... tn) must form the center of a 'cap' which is a section of the radius 4 sphere. If the diameters of the caps are formed by considering a 30° angle-width from the origin (15° on either side of the center of the cap, see figure)... then none of the caps will overlap one another.
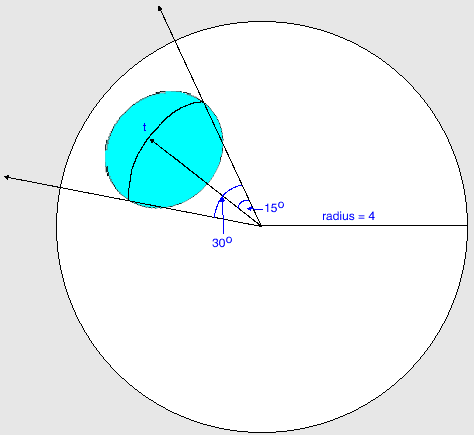
By surface of revolutions in Calculus, one can detemine the surface area of such a cap to be: 8*PI*x where x is the 'height of the cap' (the distance from it's t-center to the plane containing the cap's circular edge).
Basic trigonometry shows that x =~ 0.13629...
Now, the surface area of the radius 4 sphere is 64*PI, so no more than:
(64*PI)/(8*PI*x) caps can reside on the surface an still be mutually
disjoint.
The solved value is ~58.69... or at most 58 caps.
q.e.d.
Room for improvements?
Furthermore, I believe that the packing density of these caps upon the surface of a sphere cannot exceed the packing density of circles in a plane (which, I believe is PI*3½/6 =~ 0.9069 ).
If these two beliefs are true, that would allow us to lower the upper bound of the problem to:
(64*PI*PI*3½)/(8*PI*x*6) ... where x =~ 0.13629...
this yields: ~53.229... or at most 53 spheres (i.e.: sides to the polyhedral Voronoi Cell) about s0.
If this limit on density could be improved by considering not a general cap-on-surface approach but with the specific case of a 15° angle-radius... maybe upper bound could be lowered further. I (intuitively) see little improvement on the lower end (maybe up to 45 or 46).
Questions, comments, etc... should be sent to eric@ericharshbarger.org.
© Copyright, 1996, Eric Harshbarger
 Trying to place 12 circles equally about the central circle (to form a regular dodecagon Voronoi Cell) yields an invalid arrangement. The illustration proving its unsaturated state is quite pretty (see Figure); it was shown to me during the MH639 class by W. Kuperberg.
Trying to place 12 circles equally about the central circle (to form a regular dodecagon Voronoi Cell) yields an invalid arrangement. The illustration proving its unsaturated state is quite pretty (see Figure); it was shown to me during the MH639 class by W. Kuperberg.

